กราฟของฟังก์ชัน

(1) กราฟของฟังก์ชัน f(x) = x⁴ − 4^x บนช่วง [−2,+3] ซึ่งแสดงรากที่เป็นจำนวนจริงและจุดต่ำสุดของกราฟภายในช่วงนี้ด้วย

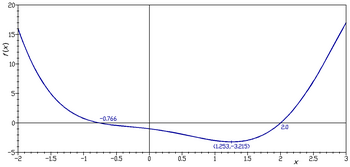
กราฟของฟังก์ชัน f (อังกฤษ: graph of a function) ในทางคณิตศาสตร์ คือการรวบรวมคู่อันดับ (x, f(x)) ทั้งหมด ถ้าฟังก์ชันรับค่า x เป็นสเกลาร์ กราฟนี้จะเป็นกราฟสองมิติ และจะกลายเป็นเส้นโค้งสำหรับฟังก์ชันต่อเนื่อง ถ้าฟังก์ชันรับค่า x เป็นคู่อันดับของจำนวนจริง (x₁, x₂) กราฟนี้จะเป็นการรวบรวมสามสิ่งอันดับ (x₁, x₂, f(x₁, x₂)) ทั้งหมด หรือเป็นกราฟสามมิติ และจะกลายเป็นพื้นผิวสำหรับฟังก์ชันต่อเนื่อง

หากกล่าวอย่างไม่เป็นทางการ ถ้า x เป็นจำนวนจริง และ f เป็นฟังก์ชันค่าจริง กราฟ อาจหมายถึงตัวแทนเชิงภาพ (graphical representation) ของการรวบรวมเหล่านี้ในรูปแบบกราฟเส้น นั่นคือเส้นโค้งบนระนาบคาร์ทีเซียน และแกนคาร์ทีเซียนเป็นต้น การวาดกราฟบนระนาบคาร์ทีเซียนบางครั้งก็อาจเรียกว่า การร่างเส้นโค้ง (curve sketching) กราฟของฟังก์ชันจำนวนจริงอาจลงจุดได้โดยตรงบนตัวแทนเชิงภาพของฟังก์ชันนั้น สำหรับฟังก์ชันทั่วไป ตัวแทนเชิงภาพไม่จำเป็นว่าจะต้องสามารถหาได้ และนิยามของกราฟของฟังก์ชันก็เพียงพอต่อความต้องการในประโยคคณิตศาสตร์ต่าง ๆ แล้ว ตัวอย่างเช่น ทฤษฎีบทกราฟปิด (closed graph theorem) ในการวิเคราะห์เชิงฟังก์ชัน

มโนทัศน์ของกราฟของฟังก์ชันสามารถวางนัยทั่วไปเป็นกราฟของความสัมพันธ์ (graph of a relation) สังเกตว่าถึงแม้ฟังก์ชันหนึ่ง ๆ สามารถระบุได้ด้วยกราฟของมันเสมอ แต่ฟังก์ชันสองฟังก์ชันที่มีโคโดเมนต่างกันก็อาจมีกราฟเหมือนกันได้ ฟังก์ชันเหล่านั้นจึงไม่ใช่ฟังก์ชันเดียวกัน ยกตัวอย่าง ฟังก์ชันพหุนามกำลังสามในตัวอย่างเป็นฟังก์ชันทั่วถึง (surjection) ถ้าโคโดเมนเป็นจำนวนจริง แต่จะไม่ใช่ฟังก์ชันทั่วถึงถ้าโคโดเมนเป็นจำนวนเชิงซ้อน

การทดสอบว่ากราฟเส้นโค้งหนึ่ง ๆ เป็นฟังก์ชันของ x หรือไม่ ให้ใช้การทดสอบเส้นแนวยืน (vertical line test) ในทางกลับกัน การทดสอบว่ากราฟเส้นโค้งหนึ่ง ๆ เป็นฟังก์ชันของ y หรือไม่ ให้ใช้การทดสอบเส้นแนวนอน (horizonal line test) ถ้าฟังก์ชันนั้นมีฟังก์ชันผกผัน กราฟของฟังก์ชันผกผันจะหาได้จากเงาสะท้อนในกระจกของกราฟของฟังก์ชันเดิม โดยมีเส้นตรง y = x เป็นแกน

ในทางวิทยาศาสตร์ วิศวกรรมศาสตร์ เทคโนโลยี การเงิน และอื่น ๆ กราฟถูกใช้เป็นเครื่องมืออเนกประสงค์ กรณีง่ายสุดคือตัวแปรหนึ่ง ๆ จะถูกลงจุด (plot) เป็นฟังก์ชันของตัวแปรอื่น โดยใช้แกนที่ตัดกันเป็นมุมฉากตามปกติ

ในรากฐานของคณิตศาสตร์สมัยใหม่อันเป็นที่รู้จักกันว่าทฤษฎีเซต ฟังก์ชันและกราฟของฟังก์ชันโดยพื้นฐานถือว่าคือสิ่งเดียวกัน

(2) กราฟของฟังก์ชัน f(x) = x³ − 9x

ตัวอย่าง

ฟังก์ชันตัวแปรเดียว

(3) กราฟของฟังก์ชัน f(x, y) = sin(x²) · cos(y²)

กราฟของฟังก์ชัน

$f(x)=\left\{{\begin{matrix}a,&{\mbox{if }}x=1\\d,&{\mbox{if }}x=2\\c,&{\mbox{if }}x=3\end{matrix}}\right.$

คือ

{ (1,a), (2,d), (3,c) }

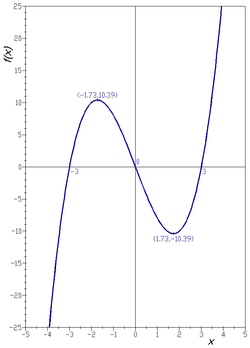
กราฟของพหุนามกำลังสามบนเส้นจำนวนจริง

$f(x)=x^{3}-9x$

คือ

{ (x, x³ − 9x) : x เป็นจำนวนจริง }

ถ้าลงจุดเซตนี้บนระนาบคาร์ทีเซียน ผลลัพธ์จะได้เส้นโค้งตามภาพ (2)

ฟังก์ชันสองตัวแปร

(4) การลงจุดของกราฟของฟังก์ชัน f(x, y) = −(cos(x²) + cos(y²))² และแสดงภาพฉายเกรเดียนต์บนระนาบข้างล่าง

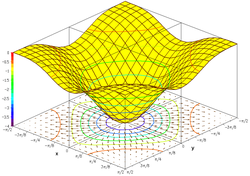
กราฟของฟังก์ชันตรีโกณมิติ

f(x, y) = sin(x²) · cos(y²)

คือ

{ (x, y, sin(x²) · cos(y²)) : x และ y เป็นจำนวนจริง }

ถ้าลงจุดเซตนี้บนระบบพิกัดคาร์ทีเซียนสามมิติ ผลลัพธ์จะได้พื้นผิวตามภาพ (3)

บางครั้งการใส่เกรเดียนต์ของฟังก์ชันและเส้นโค้งระดับไว้บนกราฟก็อาจมีประโยชน์ เส้นโค้งระดับสามารถวาดบนกราฟพื้นผิวของฟังก์ชันหรือฉายลงบนระนาบข้างล่าง

ภาพถัดมา (4) แสดงการวาดกราฟของฟังก์ชัน

f(x, y) = −(cos(x²) + cos(y²))²

แนวฉากของกราฟ

กำหนดให้ฟังก์ชัน f รับค่าตัวแปร n ตัว ได้แก่ $x=x_{1},\dotsc ,x_{n}$ แนวฉากของกราฟคือ

$(\nabla f,-1)$

(ขึ้นอยู่กับการคูณด้วยค่าคงตัว) สิ่งนี้สามารถพบได้โดยพิจารณากราฟว่าเป็นเซตระดับ (level set) ของฟังก์ชัน $g(x,z)=f(x)-z$ และการใช้ $\nabla g$ เป็นแนวฉากของเซตระดับ

การวางนัยทั่วไป

กราฟของฟังก์ชันเป็นส่วนหนึ่งของผลคูณคาร์ทีเซียนของเซต ตัวอย่างเช่น ระนาบ xy เป็นผลคูณคาร์ทีเซียนระหว่างเส้นตรงสองเส้นคือแกน x กับแกน y, ผิวทรงกระบอกเป็นผลคูณคาร์ทีเซียนระหว่างเส้นตรงกับรูปวงกลม ซึ่งความสูง รัศมี และมุมเป็นตัวกำหนดตำแหน่งที่แน่นอนของจุดต่าง ๆ มัดเส้นใย (fiber bundle) ตามปกติไม่เป็นผลคูณคาร์ทีเซียน แต่ถ้าหากมองเข้าไปใกล้ก็อาจเห็นเป็นผิวชนิดหนึ่งและนับเป็นผลคูณคาร์ทีเซียนได้ สัญกรณ์ที่สอดคล้องของกราฟบนมัดเส้นใยเรียกว่า ภาคตัด (section)

ดูเพิ่ม

• เส้นกำกับ
• แผนภูมิ
• ฟังก์ชันคองเคฟ
• ฟังก์ชันคอนเวกซ์
• เส้นชั้นความสูง

• จุดวิกฤต
• อนุพันธ์
• เอพิกราฟ
• กราฟ (คณิตศาสตร์)
• ทฤษฎีกราฟ

• ความชัน
• สมการ
• เททระวิว
• การเลื่อนขนานแนวยืน
• ระยะตัดแกน y

แหล่งข้อมูลอื่น

• Graph of function, derivative and antiderivative plotter เก็บถาวร 2016-03-18 ที่ เวย์แบ็กแมชชีน
• Weisstein, Eric W. "Function Graph." From MathWorld—A Wolfram Web Resource.