ทฤษฎีบทค่ามัชฌิม
| บทความนี้เป็นส่วนหนึ่งของ |
| แคลคูลัส |
|---|
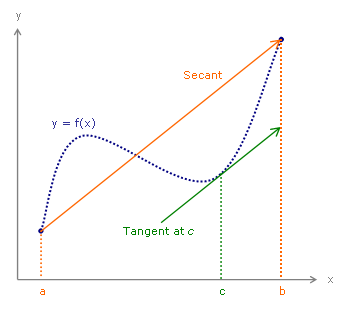
ทฤษฎีบทค่ามัชฌิมหรือทฤษฎีบทค่าเฉลี่ย (อังกฤษ: mean value theorem) เป็นทฤษฎีบทในแคลคูลัสและการวิเคราะห์เชิงจริง ซึ่งกล่าวว่า สำหรับส่วนของเส้นโค้งใด ๆ ที่กำหนดให้ จะมีจุดหนึ่งจุดอยู่บนส่วนของเส้นโค้ง ที่เส้นสัมผัส ณ จุดนั้นจะขนานกับเส้นเชื่อมจุดปลายทั้งสองข้างของเส้นโค้ง
ทฤษฎีบทค่ามัชฌิมเป็นรูปนัยทั่วไปของทฤษฎีบทของโรลล์
เนื้อหาของทฤษฎีบท
[แก้]ทฤษฎีบทค่ามัชฌิม — ให้ เป็นฟังก์ชันต่อเนื่องบนช่วงปิด และหาอนุพันธ์ได้บนช่วงเปิด แล้ว จะมี อยู่ในช่วงเปิด ที่ทำให้เส้นสัมผัสเส้นโค้งที่จุด ขนานกับเส้นตรงที่ลากผ่านจุด และ หรืออีกนัยหนึ่ง[1]
ทฤษฎีบทค่ามัชฌิมของโคชี
[แก้]รูปแบบด้านล่างเป็นนัยทั่วไปหนึ่งของทฤษฎีบทค่ามัชฌิม ซึ่งรู้จักกันในชื่อ ทฤษฎีบทค่ามัชฌิมของโคชี (Cauchy's mean value theorem) หรือ ทฤษฎีบทค่ามัชฌิมแบบขยาย (extended mean value theorem)
ทฤษฎีบทค่ามัชฌิมของโคชี — ให้ เป็นฟังก์ชันต่อเนื่องบนช่วงปิด และหาอนุพันธ์ได้บนช่วงเปิด แล้ว จะมี อยู่ในช่วงเปิด ที่ทำให้
อ้างอิง
[แก้]- ↑ Garling, D. J. H. (2013). A course in mathematical analysis. Volume 1, Foundations and elementary real analysis. Cambridge: Cambridge University Press. p. 187. ISBN 978-1-107-31469-6. OCLC 842256400.


![{\displaystyle f\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)





![{\displaystyle f,g\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/07c9cdd885f66cd36e34a6418e28444dfc32ed27)
