แมนิโฟลด์

ในคณิตศาสตร์ แมนิโฟลด์ (อังกฤษ: manifold) เป็นปริภูมิเชิงทอพอโลยีที่ใกล้ ๆ แต่ละจุดจะเหมือนปริภูมิยูคลิเดียน หรือให้รัดกุมกว่านั้นคือแมนิโฟลด์มิติ ${\textstyle n}$ หรือเรียกว่า $n$ -แมนิโฟลด์ เป็นปริภูมิเชิงทอพอโลยีที่แต่ละจุดมีย่านใกล้เคียงที่สมานสัณฐานกับเซตเปิดในปริภูมิยุคลิเดียนมิติ ${\textstyle n}$

ตัวอย่างแมนิโฟลด์หนึ่งมิติ เช่น เส้นตรงและวงกลม แต่ไม่รวมเส้นโค้งที่ตัดตัวเองเช่นรูปเลข 8 ในขณะที่แมนิโฟลด์สองมิตินิยมเรียกว่าพื้นผิว (surface) ตัวอย่างพื้นผิวเช่น ระนาบ ทรงกลม ทอรัส และรวมไปถึงขวดไคลน์ และระนาบจริงเชิงภาพฉาย

แนวคิดเรื่องแมนิโฟลด์เป็นหัวใจหลักของเรขาคณิตและฟิสิกส์เชิงคณิตศาสตร์สมัยใหม่ ทั้งนี้เพราะแมนิโฟลด์สามารถใช้อธิบายปริภูมิหรือโครงสร้างที่สลับซับซ้อนในเทอมของทอพอโลยีของปริภูมิที่ง่ายกว่าได้ นอกจากนี้อาจมองแมนิโฟลด์ว่าผลเฉลยของระบบสมการ หรือกราฟของฟังก์ชันได้ ซึ่งมีประยุกต์ใช้ในงานคอมพิวเตอร์กราฟิกส์ที่ต้องสร้างภาพจากระบบพิกัด เช่น ระบบซีทีสแกน

แมนิโฟลด์อาจมีโครงสร้างเพิ่มขึ้นมาได้อีก ตัวอย่างชั้นของแมนิโฟลด์ที่สำคัญได้แก่ แมนิโฟลด์หาอนุพันธ์ได้ (differentiable manifold) ซึ่งมีโครงสร้างหาอนุพันธ์ได้ทำให้สามารถใช้แคลคูลัสบนแมนิโฟลด์ได้ การระบุเมทริกรีมันเนียนบนแมนิโฟลด์สามารถใช้วัดระยะทางและมุมได้ แมนิโฟลด์ซิมเพลคติกเป็นปริภูมิเฟสในกลศาสตร์ดั้งเดิมรูปแบบแฮมิลโทเนียน และแมนิโฟลด์ลอเรนเซียนสี่มิติใช้จำลองปริภูมิ-เวลาในทฤษฎีสัมพัทธภาพทั่วไป

ตัวอย่างของแมนิโฟลด์

วงกลม

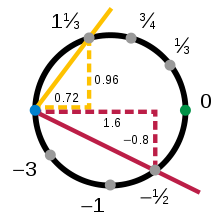
วงกลมเป็นตัวอย่างของแมนิโฟลด์ที่ง่ายที่สุดถัดจากเส้นตรง ในวิชาทอพอโลยีไม่สนใจการบิดงอ ดังนั้นชิ้นส่วนเล็ก ๆ ของวงกลมจึงมีสมบัติเชิงทอพอโลยีเหมือนกันกับเส้นตรง พิจารณาส่วนของวงกลมหนึ่งหน่วย x² + y² = 1 เฉพาะส่วนท่อนบนที่ค่าพิกัด y เป็นค่าบวก (แสดงด้วยส่วนสีเหลืองในรูป 1) ทุกจุดบนส่วนนี้สามารถระบุได้เพียงแบบเดียวโดยอาศัยค่าพิกัด x เท่านั้น

ดังนั้นการฉายส่วนของวงกลมนี้ลงบนแกน x จะเป็นการส่งที่ต่อเนื่องและหาอินเวอร์สได้จากส่วนโค้งบน (top) ไปยังช่วงเปิด (−1, 1) $\chi _{\mathrm {top} }(x,y)=x.\,$

ฟังก์ชันแบบดังกล่าว และบริเวณเปิดที่ส่งไปหาเรียกรวมกันว่า ชาร์ท (charts, แผนที่) ในทำนองเดียวกันมีชาร์ทสำหรับส่วนล่าง (bottom) ส่วนซ้าย (left) และส่วนขวา (right) ของวงกลม ${\begin{aligned}\chi _{\mathrm {bottom} }(x,y)&=x\\\chi _{\mathrm {left} }(x,y)&=y\\\chi _{\mathrm {right} }(x,y)&=y.\end{aligned}}$

รวมกันแล้วชาร์ททั้งหมดคลุมวงกลมทั้งวง และชาร์ททั้งสี่ประกอบกันเป็นแอตลาส (atlas) ของวงกลม

ชาร์ทบน $\chi _{\mathrm {top} }$ และชาร์ทขวา $\chi _{\mathrm {right} }$ ต่างมีส่วนทับกันบนโดเมนของมัน จะเห็นว่าเป็นบริเวณซ้อนทับระหว่างสีเหลืองและสีเขียว ซึ่งเป็นส่วนของวงกลมที่พิกัด $x$ และ $y$ เป็นบวกทั้งคู่ ชาร์ททั้งสองส่งส่วนซ้อนทับนี้ไปบนช่วง $(0,1)$ แต่ว่าส่งต่างกัน ดังนั้นเราอาจพิจารณาฟังก์ชัน $T:(0,1)\rightarrow (0,1)=\chi _{\mathrm {right} }\circ \chi _{\mathrm {top} }^{-1}$ ได้

ให้ a เป็นจำนวนจริงใด ๆ ในช่วง $(0,1)$ แล้ว: ${\begin{aligned}T(a)&=\chi _{\mathrm {right} }\left(\chi _{\mathrm {top} }^{-1}\left[a\right]\right)\\&=\chi _{\mathrm {right} }\left(a,{\sqrt {1-a^{2}}}\right)\\&={\sqrt {1-a^{2}}}\end{aligned}}$

ฟังก์ชัน $T$ แบบข้างต้นเรียกว่า transition map

ชาร์ททั้งสี่ไม่ใช่แอตลาสเดียวที่เป็นไปได้สำหรับวงกลม พิจารณาชาร์ท $\chi _{\mathrm {minus} }(x,y)=s={\frac {y}{1+x}}$ และ $\chi _{\mathrm {plus} }(x,y)=t={\frac {y}{1-x}}$

ในที่นี้ s คือความชันของเส้นตรงที่ผ่านจุด (x, y) และจุด (−1, 0) ในทำนองเดียวกัน t เป็นค่าลบของความชันของเส้นตรงที่ผ่านพิกัด (x, y) และ (+1, 0) จะได้การส่งอินเวอร์สจาก s ไปยัง (x, y) นั้นกำหนดโดย ${\begin{aligned}x&={\frac {1-s^{2}}{1+s^{2}}}\\[5pt]y&={\frac {2s}{1+s^{2}}}\end{aligned}}$

สามารถตรวจสอบได้ว่า x² + y² = 1 สำหรับทุกค่า s และ t ชาร์ททั้งสองเป็นแอตลาสอันที่สองสำหรับวงกลม โดยมี transition map คือ $t={\frac {1}{s}}$ (สำหรับทุกจุดที่ทั้ง s และ t ไม่เป็นศูนย์)

แต่ละชาร์ทจะไม่มีจุดอยู่หนึ่งจุด ได้แก่ (−1, 0) สำหรับ s หรือ (+1, 0) สำหรับ t ตามลำดับ ฉะนั้นชาร์ทเดียวจึงไม่สามารถคลุมวงกลมทั้งวงได้ และสามารถพิสูจน์ได้ว่าไม่มีชาร์ทเดียวอันใดสามารถคลุมวงกลมได้ทั้งหมด

ทรงกลม

ทรงกลมเป็นตัวอย่างของพื้นผิว ทรงกลมหนึ่งหน่วยที่กำหนดโดยสมการโดยปริยาย

x 2 + y 2 + z 2 - 1 = 0

สามารถใช้ชาร์ทหกอันคลุมได้ดังนี้ ระนาบ $z = 0$ จะตัดทรงกลมออกเป็นสองครึ่ง ( $z > 0$ และ $z < 0$ ) ซึ่งสามารถส่งไปยังดิสก์ $x 2 + y 2 < 1$ ด้วยการฉายลงบนระนาบ $xy$ ทำให้ได้ชาร์ทสองอัน และอีกสี่ชาร์ทที่เหลือนั้นทำคล้าย ๆ กัน

เช่นเดียวกันกับวงกลม เราอาจหาชาร์ทที่เกือบคลุมทั้งทรงกลมเว้นแต่เพียงจุดหนึ่ง ฉะนั้นสองชาร์ทนั้นเพียงพอในการคลุมทรงกลม แต่ไม่สามารถทำได้ด้วยชาร์ทเดียว

ตัวอย่างนี้สำคัญในทางประวัติศาสตร์ และเป็นที่มาของคำว่าชาร์ทและแอตลาส พื้นผิวของโลกไม่สามารถทำออกมาเป็นแผนที่ระนาบเพียงอันเดียวได้ ฉะนั้นต้องใช้แอตลาสหรือสมุดแผนที่ (atlas) เพื่อครอบคลุมพื้นผิวของโลกทั้งหมด

เส้นโค้งอื่น ๆ

แมนิโฟลด์ไม่จำเป็นต้องเป็นปริภูมิเชื่อมโยง (ติดกันเป็นชิ้นเดียว) ตัวอย่างเช่น วงกลมสองวงเป็นแมนิโฟลด์ และแมนิโฟลด์ไม่จำเป็นต้องเป็นเซตปิด ฉะนั้นส่วนของเส้นตรงที่ไม่มีจุดปลายก็เป็นแมนิโฟลด์

ตัวอย่างของแมนิโฟลด์ เช่น พาราโบลา, ไฮเพอร์โบลา และทางเดินของจุดบนเส้นโค้งกำลังสาม y² = x³ − x ซึ่งมีสองส่วน

ตัวอย่างของปริภูมิที่ไม่ใช่แมนิโฟลด์เช่น รูปเลข 8 ซึ่งไม่มีชาร์ทที่เหมาะสมสำหรับจุดตัดของวงกลมทั้งสองได้

นิยามทางคณิตศาสตร์

ถ้าจะกล่าวโดยง่าย แมนิโฟลด์คือปริภูมิที่จำลองมาจากปริภูมิยูคลิเดียน แมนิโฟลด์อื่นที่ศึกษาเกิดจากการระบุโครงสร้างเพิ่มเติมไปบนแมนิโฟลด์เชิงทอพอโลยีซึ่งจะได้นิยามด้านล่าง

แมนิโฟลด์เชิงทอพอโลยี

ให้ $X$ เป็นปริภูมิเชิงทอพอโลยี จะกล่าวว่า $X$ เป็นแมนิโฟลด์เชิงทอพอโลยี (topological manifold) หากมีสมบัติดังต่อไปนี้

$X$ เป็นปริภูมิเฮาสดอร์ฟฟ์ (Hausdorff space)
$X$ เป็นปริภูมินับได้อันดับสอง (second countable)
$X$ สมานสัณฐานเฉพาะที่กับปริภูมิยูคลิเดียนมิติ $n$ (locally homeomorphic to $\mathbb {R} ^{n}$ )

เงื่อนไขการเป็นเป็นปริภูมิเฮาสดอร์ฟฟ์และการเป็นปริภูมินับได้อันดับสองเป็นเงื่อนไขทางทอพอโลยีที่ตัดกรณีที่ "ไม่เหมาะ" จะพิจารณาเช่น เส้นตรงยาว (long line) หรือเส้นตรงที่มีจุดกำเนิดสองจุด (line with two origins)

เงื่อนไขที่เสนอว่าแมนิโฟลด์จำลองมาจากปริภูมิยูคลิเดียน คือการที่ $X$ สมานสัณฐานเฉพาะที่กับปริภูมิยูคลิเดียนมิติ $n$ นั่นคือแต่ละจุดจะมีย่านใกล้เคียงที่สมานสัณฐานกับปริภูมิยูคลิเดียนมิติ $n$ สำหรับบางจำนวนนับ $n$ ภาวะสมานสัณฐานสื่อถึงการมีคุณสมบัติเชิงทอพอโลยีเหมือน ๆ กันระหว่างปริภูมิยูคลิเดียนและย่านใกล้เคียงรอบแต่ละจุด

ค่า $n$ ที่ปรากฎเรียกว่ามิติเฉพาะที่ (local dimension) ของแมนิโฟลด์เชิงทอพอโลยี โดยทั่วไปเรากำหนดให้แมนิโฟลด์จะต้องมีมิติเฉพาะที่เท่ากันทุกจุด ซึ่งเป็นจริงสำหรับแมนิโฟลด์เชื่อมโยง แต่หนังสือบางเล่มอาจยอมให้แมนิโฟลด์ไม่จำเป็นต้องเป็นปริภูมิเชื่อมโยง และแต่ละจุดอาจจะมีมิติที่แตกต่างกัน^[1]

ในมุมมองทางทฤษฎีชีฟ แมนิโฟลด์เชิงทอพอโลยีเป็นปริภูมิมีริงเฉพาะที่ (locally ringed space) ที่มีชีฟโครงสร้างที่สมสัณฐานเฉพาะที่กับชีฟของฟังก์ชันต่อเนื่องบนปริภูมิยูคลิเดียน นี่เป็นมุมมองสำหรับแมนิโฟลด์ในเรขาคณิตเชิงพีชคณิต

หมายเหตุ

↑ E.g. see Riaza, Ricardo (2008), Differential-Algebraic Systems: Analytical Aspects and Circuit Applications, World Scientific, p. 110, ISBN 9789812791818; Gunning, R. C. (1990), Introduction to Holomorphic Functions of Several Variables, Volume 2, CRC Press, p. 73, ISBN 9780534133092.

อ้างอิง

Freedman, Michael H., and Quinn, Frank (1990) Topology of 4-Manifolds. Princeton University Press. ISBN 0-691-08577-3.
Guillemin, Victor and Pollack, Alan (1974) Differential Topology. Prentice-Hall. ISBN 0-13-212605-2. Advanced undergraduate / first-year graduate text inspired by Milnor.
Hempel, John (1976) 3-Manifolds. Princeton University Press. ISBN 0-8218-3695-1.
Hirsch, Morris, (1997) Differential Topology. Springer Verlag. ISBN 0-387-90148-5. The most complete account, with historical insights and excellent, but difficult, problems. The standard reference for those wishing to have a deep understanding of the subject.
Kirby, Robion C. and Siebenmann, Laurence C. (1977) Foundational Essays on Topological Manifolds. Smoothings, and Triangulations. Princeton University Press. ISBN 0-691-08190-5. A detailed study of the category of topological manifolds.
Lee, John M. (2000) Introduction to Topological Manifolds. Springer-Verlag. ISBN 0-387-98759-2. Detailed and comprehensive first-year graduate text.
Lee, John M. (2003) Introduction to Smooth Manifolds. Springer-Verlag. ISBN 0-387-95495-3. Detailed and comprehensive first-year graduate text; sequel to Introduction to Topological Manifolds.
Massey, William S. (1977) Algebraic Topology: An Introduction. Springer-Verlag. ISBN 0-387-90271-6.
Milnor, John (1997) Topology from the Differentiable Viewpoint. Princeton University Press. ISBN 0-691-04833-9. Classic brief introduction to differential topology.
Munkres, James R. (1991) Analysis on Manifolds. Addison-Wesley (reprinted by Westview Press) ISBN 0-201-51035-9. Undergraduate text treating manifolds in $\mathbb {R} ^{n}$ .
Munkres, James R. (2000) Topology. Prentice Hall. ISBN 0-13-181629-2.
Neuwirth, L. P., ed. (1975) Knots, Groups, and 3-Manifolds. Papers Dedicated to the Memory of R. H. Fox. Princeton University Press. ISBN 978-0-691-08170-0.
Riemann, Bernhard, Gesammelte mathematische Werke und wissenschaftlicher Nachlass, Sändig Reprint. ISBN 3-253-03059-8.
- Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse. The 1851 doctoral thesis in which "manifold" (Mannigfaltigkeit) first appears.
- Ueber die Hypothesen, welche der Geometrie zu Grunde liegen. The 1854 Göttingen inaugural lecture (Habilitationsschrift).
Spivak, Michael (1965) Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus. W.A. Benjamin Inc. (reprinted by Addison-Wesley and Westview Press). ISBN 0-8053-9021-9. Famously terse advanced undergraduate / first-year graduate text.
Spivak, Michael (1999) A Comprehensive Introduction to Differential Geometry (3rd edition) Publish or Perish Inc. Encyclopedic five-volume series presenting a systematic treatment of the theory of manifolds, Riemannian geometry, classical differential geometry, and numerous other topics at the first- and second-year graduate levels.
Tu, Loring W. (2011). An Introduction to Manifolds (2nd ed.). New York: Springer. ISBN 978-1-4419-7399-3.. Concise first-year graduate text.

แหล่งข้อมูลอื่น

Hazewinkel, Michiel, บ.ก. (2001), "Manifold", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Dimensions-math.org (A film explaining and visualizing manifolds up to fourth dimension.)
The manifold atlas project of the Max Planck Institute for Mathematics in Bonn

[1] E.g. see Riaza, Ricardo (2008), Differential-Algebraic Systems: Analytical Aspects and Circuit Applications, World Scientific, p. 110, ISBN 9789812791818; Gunning, R. C. (1990), Introduction to Holomorphic Functions of Several Variables, Volume 2, CRC Press, p. 73, ISBN 9780534133092.

[1]