แฟร็กทัล

ภาพแฟร็กทัล จาก เซตม็องแดลโบรต, วาดโดยการพล็อตสมการวนซ้ำไปเรื่อย ๆ

แฟร็กทัล หรือ สาทิสรูป (อังกฤษ: fractal) ในปัจจุบันเป็นคำที่ใช้ในเชิงวิทยาศาสตร์และคณิตศาสตร์ หมายถึง วัตถุทางเรขาคณิต ที่มีคุณสมบัติคล้ายตนเอง คือ ดูเหมือนกันไปหมด (เมื่อพิจารณาจากแง่ใดแง่หนึ่ง) ไม่ว่าจะดูที่ระดับความละเอียด (โดยการส่องขยาย) หรือ สเกลใดก็ตาม

คำว่า แฟร็กทัล นี้ เบอนัว ม็องแดลโบรต เป็นคนบัญญัติขึ้นในปี ค.ศ. 1975 จากคำว่า fractus ในภาษาละติน ซึ่งแปลว่า แตก หรือ ร้าว

ประวัติ

เกล็ดหิมะค็อค

ได้มีการค้นพบสิ่งที่เรารู้จักกันในนามของแฟร็กทัลมานานก่อนที่คำว่า "แฟร็กทัล" จะได้รับการบัญญัติขึ้นมาใช้เรียกสิ่งเหล่านี้ ในปี ค.ศ. 1872 คาร์ล ไวเออร์ชตรัสส์ (Karl Weierstrass) ได้ยกตัวอย่างของฟังก์ชัน ที่มีคุณสมบัติ "everywhere continuous but nowhere differentiable" คือ มีความต่อเนื่องที่ทุกจุด แต่ไม่สามารถหาค่าอนุพันธ์ได้ ต่อมาในปี ค.ศ. 1904 เฮลเก ฟอน ค็อค (Helge von Koch) ได้ยกตัวอย่างทางเรขาคณิต ซึ่งได้รับการเรียกขานในปัจจุบันนี้ว่า "เกล็ดหิมะค็อค" (Koch snowflake) ต่อมาในปี ค.ศ. 1938 พอล ปีแอร์ ลาวี (Paul Pierre Lévy) ได้ทำการศึกษา รูปร่างของ กราฟ (curve และ surface) ซึ่งมีคุณสมบัติที่ส่วนประกอบย่อย มีความเสมือนกับโครงสร้างโดยรวมของมัน คือ "Lévy C curve" และ "Lévy dragon curve"

เกออร์ก คันทอร์ (Georg Cantor) ก็ได้ยกตัวอย่างของ เซตย่อยของจำนวนจริง ซึ่งมีคุณสมบัติแฟร็กทัลนี้ เป็นที่รู้จักกันในชื่อ เซตคันทอร์ หรือ ฝุ่นคันทอร์ จากการศึกษาเซตคันทอร์นี้ นักคณิตศาสตร์ เช่น Constantin Carathéodory และ Felix Hausdorff ได้ขยายความแนวคิดเรื่อง มิติ (dimension) จากเดิมที่เป็นจำนวนเต็ม ให้ครอบคลุมถึงมิติที่ไม่เป็นจำนวนเต็ม นอกจากนั้น นักคณิตศาสตร์อีกหลายคน ในช่วงปลายคริสต์ศตวรรษที่ 19 ถึงต้นคริสต์ศตวรรษที่ 20 เช่น อองรี ปวงกาเร, เฟลิกซ์ คลิน (Felix Klein), ปิแอร์ ฟาตู (Pierre Fatou) และ กาสตง จูเลีย (Gaston Julia) ได้ศึกษาฟังก์ชันวนซ้ำ (Iterated function) ซึ่งมีความเกี่ยวพันอย่างใกล้ชิดกับ คุณสมบัติความคล้ายตนเอง (self-similarity) แต่บุคคลเหล่านั้นก็ไม่ได้เห็นถึงความสวยงามของภาพจาก itereated functions ที่เราได้เห็นกัน เนื่องจากการแสดงผลที่ต้องใช้เทคโนโลยีคอมพิวเตอร์กราฟิก ซึ่งพัฒนาขึ้นในภายหลัง

ในปี ค.ศ. 1960 เบอนัว ม็องแดลโบรต ได้ทำการศึกษาถึงคุณสมบัติความคล้ายตนเอง นี้ และตีพิมพ์บทความชื่อ How Long is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. แมนดัลบรอ ได้เห็นถึงความสัมพันธ์ของผลงานในเรื่องต่าง ๆ ในอดีต ซึ่งดูราวกับจะเป็นคนละเรื่องไม่มีความสัมพันธ์กัน เขาได้รวบรวมแนวความคิด และบัญญัติคำว่า แฟร็กทัล ขึ้น เพื่อใช้ระบุถึงวัตถุที่มีคุณสมบัติความคล้ายตนเอง

คำจำกัดความ

เซตจูเลีย

แฟร็กทัล นั้นนอกจากเป็นวัตถุที่มี ความคล้ายตนเอง แล้วยังมีอีกคุณสมบัติหนึ่งคือ มีมิติเฮาส์ดอร์ฟ (Hausdorff) ไม่เป็นจำนวนเต็ม (นิยามโดย เบอนัว ม็องแดลโบรต ไว้ว่า A fractal is by definition a set for which the Hausdorff-Besicovitch dimension strictly exceeds the topological dimension.) แต่คำจำกัดความนี้ดูเหมือนจะมีปัญหาอยู่มาก เนื่องจาก ปรากฏว่ามีวัตถุที่มีรูปร่างเป็นแฟร็กทัล แต่ไม่ได้เป็นไปตามคุณสมบัติมิตินี้

คำจำกัดความของสิ่งที่เราเรียกว่า แฟร็กทัล นั้นจะค่อนข้างกำกวม ไม่ชัดเจนเนื่องจาก

• สิ่งที่เราพิจารณาอยู่ในขอบข่ายของ แฟร็กทัล นั้นจะเป็นสิ่งที่ "irregular" หรือ ไม่สม่ำเสมอ คือไม่อยู่ในขอบข่ายที่จะพิจารณาด้วย เรขาคณิตแบบดั้งเดิมได้ แต่ว่าขอบข่ายของความไม่สม่ำเสมอที่เราพิจารณานั้น ไม่สามารถระบุให้ชัดเจนได้
• คุณสมบัติความคล้ายตนเอง นั้น มองได้หลายแง่มุม ความเหมือนนั้นเหมือนได้หลายแง่ เช่น นอกจากเหมือนกันทุกประการ ยังมีเหมือนในเชิงสถิติ และอื่น ๆ ซึ่งทำให้คำจำกัดความนั้นไม่สามารถระบุเด่นชัดลงไปได้
• เมื่อมองในแง่ของการสร้างแฟร็กทัลโดยการใช้โครงสร้างทำซ้ำ หรือ recursive จะเห็นว่าเราสามารถจะระบุแฟร็กทัลนั้น ด้วยโครงสร้าง recursive ของมันได้ แต่ในความเป็นจริง มีเพียงบางแฟร็กทัลเท่านั้น ที่เราสามารถระบุด้วยโครงสร้าง recursive ได้

ประเภทของแฟร็กทัลและตัวอย่าง

วิธีการสร้างเกล็ดหิมะค็อค 4 ขั้นตอนแรก

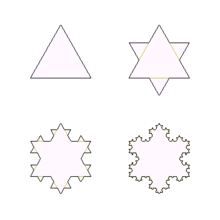
แฟร็กทัลสามารถจำแนกออกเป็นสามประเภทตามวิธีการสร้างดังนี้

แฟร็กทัลประเภทแรกมีรูปแบบการสร้างแบบง่าย ๆ โดยอาศัยหลักการวนซ้ำกฎเกณฑ์ที่กำหนดไปเรื่อย ๆ ไม่มีที่สิ้นสุด เช่น เซตคันทอร์, ฝุ่นคันทอร์ และ ฟังก์ชันคันทอร์ ซึ่งจัดเป็นหนึ่งในฟังก์ชันประเภทที่เรียกว่า Devil's staircase, เส้นโค้งค็อค และ เกล็ดหิมะค็อค, พรมซูร์พินสกี (Sierpinski carpet), สามเหลี่ยมซูร์พินสกี (Sierpinski triangle) Space-filling curve หรือ Peano curve และ เส้นโค้งมังกร เป็นต้น แฟร็กทัลประเภทนี้มีคุณสมบัติคล้ายตนเองอย่างสมบูรณ์ (exact self-similarity)

แฟร็กทัลอีกจำนวนหนึ่งมีที่มาจากการศึกษาทฤษฎีความอลวน เรียกว่า escape-time fractal ตัวอย่างเช่น เซตจูเลีย, เซตม็องแดลโบรต, แฟร็กทัล Burning Ship และ แฟร็กทัลไลยาปูนอฟ (Lyapunov) แฟร็กทัลสร้างจากวนซ้ำสมการ $f_{c}(z)$ ไปเรื่อย ๆ หรือเขียนอยู่ในรูปสัญลักษณ์ทางคณิตศาสตร์คือ $f_{c}(f_{c}(f_{c}(...)))$ และสร้างกราฟของค่าพารามิเตอร์ $c$ หรือค่าเริ่มต้นของ $z$ ที่ให้ผลลัพธ์ที่อลวน แฟร็กทัลเหล่านี้มักมีคุณสมบัติคล้ายตนเองที่ไม่สมบูรณ์ กล่าวคือ เมื่อขยายแฟร็กทัลดูส่วนที่เล็กลงจะพบว่ามีรูปร่างคล้ายแต่ไม่เหมือนรูปร่างของเดิมซะทีเดียว (quasi-self-similarity)

แฟร็กทัลที่จำลองแบบผิวหน้าของภูเขา สร้างโดยการสุ่ม

แฟร็กทัลประเภทสุดท้าย สร้างโดยกระบวนการสโตคาสติก หรือ การสุ่ม เช่น การเคลื่อนที่แบบบราวเนียน ต้นไม้บราวเนียน เป็นต้น แฟร็กทัลลักษณะนี้ เฉพาะค่าทางสถิติของแฟร็กทัลที่สเกลต่าง ๆ เท่านั้นที่มีลักษณะเหมือนกัน (statistical self-similarity)

แฟร็กทัลในธรรมชาติ

ภาพใบเฟิร์นที่สร้างโดยคอมพิวเตอร์โดยเทคนิกแฟร็กทัล

สิ่งที่มีลักษณะใกล้เคียงกับแฟร็กทัลสามารถพบได้ง่ายในธรรมชาติ ตัวอย่างสิ่งของที่มีคุณลักษณะความคล้ายตนเองในระดับหนึ่ง เช่น เมฆ เกล็ดหิมะ ภูเขา สายฟ้าในฟ้าผ่า การแตกสาขาของแม่น้ำ ปุ่มบนดอกกะหล่ำ การแตกแขนงของเส้นเลือดฝอย เป็นต้น ซึ่งเมื่อนำวัตถุนั้นมาขยายแล้วจะพบว่ามีรูปร่างคล้ายกับของเดิม แต่วัตถุในธรรมชาติก็มีข้อจำกัดคือเมื่อขยายมาก ๆ เช่น จนถึงระดับ เซลล์ หรือ โมเลกุล จะไม่เหลือคุณสมบัติความคล้ายตนเองเหลืออยู่

ต้นไม้และเฟิร์น ก็มีคุณสมบัติแฟร็กทัลในธรรมชาติของมัน เช่น กิ่งของต้นไม้ดูคล้ายต้นไม้ทั้งต้นแต่มีขนาดเล็กลง ส่วนย่อย ๆ ของใบเฟิร์นก็เช่นกัน ด้วยคุณสมบัติความคล้ายตนเองนี้ เราสามารถสร้างแบบจำลองของต้นไม้และในเฟิร์นบนเครื่องคอมพิวเตอร์ได้ง่ายโดยวิธีวนซ้ำ

แฟร็กทัลในทางศิลปะ

แฟร็กทัลยังพบได้ในงานศิลปะ ตัวอย่างเช่นภาพเขียนของจิตรกรชาวอเมริกัน แจ็คสัน พอลล็อก (Jackson Pollock) ซึ่งดูผิวเผินจะประกอบด้วยหยดหมึกหรือแต้มหมึกที่ไม่เป็นระเบียบ แต่จากการวิเคราะห์ด้วยคอมพิวเตอร์ก็พบรูปแบบของแฟร็กทัลในงานของเขา

แฟร็กทัลยังพบได้มากในศิลปะและสถาปัตยกรรมในแบบแอฟริกา เช่น บ้านรูปวงกลมเล็ก ๆ ตั้งเรียงกันเป็นรูปวงกลมใหญ่ขึ้นและใหญ่ขึ้น บ้านรูปสี่เหลี่ยมซึ่งมีรูปสี่เหลี่ยมขนาดเล็กประกอบ เป็นต้น ลวดลายของรูปร่างหนึ่ง ๆ ในหลายสเกลยังพบในสิ่งทอ รูปปั้น หรือแม้กระทั่งทรงผมในแบบแอฟริกัน

• 
  แฟร็กทัลเกิดขึ้นเมื่อดึงแผ่นอคริลิกที่ติดกันด้วยกาวออกจากกัน
• 
  การป้อนไฟฟ้าแรงสูงให้กับก้อนอคริลิกจนแตกให้เห็นรูปแฟร็กทัลที่เรียกว่า Lichtenberg figure
• 
  แฟร็กทัลที่เกิดขึ้นจากรอยแตกบนผิวของแผ่นดีวีดีเมื่อโดนรังสีจากไมโครเวฟ
• 
  กะหล่ำดอกเจดีย์มีลักษณะของแฟร็กทัล
• 
  การงอกของผลึกทองแดงในสารละลายคอปเปอร์ซัลเฟตในการชุบโลหะด้วยไฟฟ้า
• 
  ภาพขยาย phoenix set

การประยุกต์ใช้งาน

ชุดพรางที่ลายสร้างจากแฟร็กทัล

สายอากาศแบบ log-periodic

ทฤษฎีและผลจากการศึกษาแฟร็กทัล สามารถนำมาประยุกต์ใช้กับงานหลาย ๆ ด้าน ตัวอย่างที่สำคัญเช่น

การสร้างภาพในคอมพิวเตอร์ สามารถใช้กฎเกณฑ์การเรียกตนเอง (recursion) มาเขียนโปรแกรมสร้างภาพของสิ่งต่าง ๆ ที่โดยธรรมชาติมีลักษณะใกล้เคียงแฟร็กทัล เช่น ต้นไม้ ภูเขา มาใส่ในเกมคอมพิวเตอร์ หรือสร้างเป็นฉากกราฟิกส์ในภาพยนตร์ โดยโปรแกรมที่เขียนจากหลักการเรียกตนเองมีขนาดเล็ก ในทางกลับกันเราสามารถใช้แฟล็กทัลมาประยุกต์กับการบีบอัดข้อมูลสัญญาณและภาพ โดยการหาค่าพารามิเตอร์ของสมการวนซ้ำที่ให้ได้ผลลัพธ์ใกล้เคียงกับสัญญาณหรือภาพที่ต้องการ และใช้ค่าพารามิเตอร์นั้นเป็นข้อมูลที่ถูกบีบแล้ว

เราสามารถใช้วนซ้ำมาสังเคราห์เสียงดนตรีแนวใหม่ สร้างงานศิลปะแปลกใหม่ ออกแบบแฟชั่น ลวดลายบนชุดพรางตัวของทหารนาวิกโยธินสหรัฐที่เรียกว่า MARPAT (MARine Disruptive PATtern) ซึ่งมีลวดลายไม่เป็นระเบียบ สามารถกลมกลืนกับธรรมชาติได้ดี ก็สร้างขึ้นจากหลักการแฟล็กทัล

รอยร้าวต่าง ๆ ลักษณะแตกแขนงย่อย ๆ ออกไปเหมือนแฟร็กทัล จึงมีประโยชน์ในการคาดคะเนการแตกหักในวิชากลศาสตร์ (Fracture mechanics) และใช้ในการศึกษาด้านแผ่นดินไหว (Seismology)

อีกตัวอย่างการใช้งาน คือ สายอากาศแบบแฟร็กทัล ที่มีขนาดเล็กแต่สามารถรับส่งคลื่นความถี่ได้หลากหลาย สายอากาศที่ใช้รับสัญญาณโทรทัศน์ ก็มีลักษณะความคล้ายตนเองเช่นเดียวกัน

ดูเพิ่ม

• ทฤษฎีความอลวน

อ่านเพิ่ม

• Barnsley, Michael F.; and Rising, Hawley; Fractals Everywhere. Boston: Academic Press Professional, 1993. ISBN 0-12-079061-0
• Duarte, German A.; Fractal Narrative. About the Relationship Between Geometries and Technology and Its Impact on Narrative Spaces. Bielefeld: Transcript, 2014. ISBN 978-3-8376-2829-6
• Falconer, Kenneth; Techniques in Fractal Geometry. John Wiley and Sons, 1997. ISBN 0-471-92287-0
• Jürgens, Hartmut; Peitgen, Heinz-Otto; and Saupe, Dietmar; Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, 1992. ISBN 0-387-97903-4
• Mandelbrot, Benoit B.; The Fractal Geometry of Nature. New York: W. H. Freeman and Co., 1982. ISBN 0-7167-1186-9
• Peitgen, Heinz-Otto; and Saupe, Dietmar; eds.; The Science of Fractal Images. New York: Springer-Verlag, 1988. ISBN 0-387-96608-0
• Pickover, Clifford A.; ed.; Chaos and Fractals: A Computer Graphical Journey – A 10 Year Compilation of Advanced Research. Elsevier, 1998. ISBN 0-444-50002-2
• Jones, Jesse; Fractals for the Macintosh, Waite Group Press, Corte Madera, CA, 1993. ISBN 1-878739-46-8.
• Lauwerier, Hans; Fractals: Endlessly Repeated Geometrical Figures, Translated by Sophia Gill-Hoffstadt, Princeton University Press, Princeton NJ, 1991. ISBN 0-691-08551-X, cloth. ISBN 0-691-02445-6 paperback. "This book has been written for a wide audience..." Includes sample BASIC programs in an appendix.
• Sprott, Julien Clinton (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 978-0-19-850839-7.
• Wahl, Bernt; Van Roy, Peter; Larsen, Michael; and Kampman, Eric; Exploring Fractals on the Macintosh, Addison Wesley, 1995. ISBN 0-201-62630-6
• Lesmoir-Gordon, Nigel; The Colours of Infinity: The Beauty, The Power and the Sense of Fractals. 2004. ISBN 1-904555-05-5 (The book comes with a related DVD of the Arthur C. Clarke documentary introduction to the fractal concept and the Mandelbrot set.)
• Liu, Huajie; Fractal Art, Changsha: Hunan Science and Technology Press, 1997, ISBN 9787535722348.
• Gouyet, Jean-François; Physics and Fractal Structures (Foreword by B. Mandelbrot); Masson, 1996. ISBN 2-225-85130-1, and New York: Springer-Verlag, 1996. ISBN 978-0-387-94153-0. Out-of-print. Available in PDF version at."Physics and Fractal Structures" (ภาษาฝรั่งเศส). Jfgouyet.fr. สืบค้นเมื่อ October 17, 2010.
• Falconer, Kenneth (2013). Fractals, A Very Short Introduction. Oxford University Press.

แหล่งข้อมูลอื่น

• Fractals ที่ Library of Congress Web Archives (เก็บถาวร พฤศจิกายน 16, 2001)
• "Hunting the Hidden Dimension", PBS NOVA, first aired August 24, 2011
• Benoit Mandelbrot: Fractals and the Art of Roughness (เก็บถาวร กุมภาพันธ์ 17, 2014 ที่ เวย์แบ็กแมชชีน), TED, February 2010
• Technical Library on Fractals for controlling fluid
• Equations of self-similar fractal measure based on the fractional-order calculus（2007）