เส้นโค้งปิดเสมือนเวลา

ในวิชาฟิสิกส์เชิงคณิตศาสตร์, เส้นโค้งปิดเสมือนเวลา (CTC) คือ เส้นโลก (world line) ที่อยู่ในลอเรนท์เซียน แมนิโฟลด์ (Lorentzian manifold), ของอนุภาควัตถุในปริภูมิ-เวลา ซึ่งอยู่ในสภาพ "ปิด", ที่ย้อนกลับไปยังจุดเริ่มต้นเดิมของมันเอง ความเป็นไปได้นี้ถูกค้นพบโดย คูร์ท เกอเดิล (Kurt Gödel) ในปี 1949, ผู้ค้นพบวิธีการแก้สมการของสัมพัทธภาพทั่วไป (GR) ที่ช่วยให้ CTCs เป็นที่รู้จักกันว่าเป็นเกอเดิล เมตริกซ์ (Gödel metric); และตั้งแต่นั้นมาการแก้ปัญหาแบบสัมพัทธภาพทั่วไป (GR solution) อื่น ๆ ที่ประกอบด้วย CTCs จึงได้รับการค้นพบ, เช่น ทรงกระบอกทิปเลอร์ (Tipler cylinder) และ รูหนอนทะลุได้ (traversable wormhole) หาก CTCs มีอยู่จริง, การดำรงอยู่ของพวกมันก็ดูเหมือนจะบ่งบอกถึงอย่างน้อยที่สุดของความเป็นไปได้ทางทฤษฎีของการเดินทางข้ามเวลาย้อนกลับไปในอดีตในเวลาที่กำลังเกิดความพิศวงของปรากฏการณ์ปฏิทรรศน์คุณปู่, แม้ว่าหลักความสอดคล้องในตัวเองของนาวิคอฟดูเหมือนว่าจะแสดงให้เห็นว่าปฏิทรรศน์หรือความขัดแย้งดังกล่าวอาจจะเป็นสิ่งที่หลีกเลี่ยงได้ นักฟิสิกส์บางคนคิดว่า CTCs ที่ปรากฏในการแก้ปัญหา GR บางอย่างอาจถูกตัดออกจากทฤษฎีในอนาคตของแรงโน้มถ่วงควอนตัมซึ่งจะเข้ามาแทนที่ GR

กรวยแสง

กรวยแสงส่วนล่างเป็นลักษณะเฉพาะของกรวยแสงในปริภูมิแบน—พิกัดปริภูมิ-เวลาทั้งหมดที่รวมอยู่ในกรวยแสงจะมีเวลาที่ตามมาทีหลัง กรวยแสงด้านบนไม่เพียงแต่รวมตำแหน่งเชิงพื้นที่อื่น ๆ ในเวลาเดียวกันเท่านั้น แต่ยังไม่รวมถึง $x=0$ ในเวลาในอนาคตด้วย และรวมเวลาที่ผ่านมาก่อนหน้านี้ด้วย (The lower light cone is characteristic of light cones in flat space—all spacetime coordinates included in the light cone have later times. The upper light cone not only includes other spatial locations at the same time, but also does not include $x=0$ at future times, and includes earlier times.)

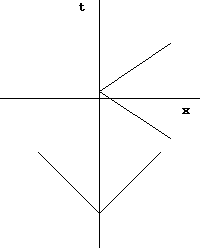
เมื่อพูดถึงพัฒนาการของระบบในสัมพัทธภาพทั่วไปหรือปริภูมิแบบมินคอฟสกีที่มากขึ้นโดยเฉพาะเป๊นพิเศษ, นักฟิสิกส์มักจะอ้างถึง "กรวยแสง" กรวยแสงแสดงให้เห็นถึงพัฒนาการในอนาคตที่เป็นไปได้ของวัตถุที่ได้รับสถานะปัจจุบันของมันหรือความเป็นไปได้ทุก ๆ ตำแหน่งที่ตั้งที่ได้รับอันเป็นตำแหน่งที่ตั้ง ณ ปัจจุบันของมัน ตำแหน่งที่ตั้งในอนาคตที่เป็นไปได้ของวัตถุจะถูก จำกัด ด้วยอัตราเร็วที่วัตถุจะสามารถเคลื่อนที่ได้, ซึ่งเป็นอัตราเร็วที่ดีที่สุดของแสง ยกตัวอย่างเช่น วัตถุที่อยู่ในตำแหน่ง P ที่เวลา t₀ สามารถเคลื่อนย้ายไปยังตำแหน่งภายใน p + c(t₁ − t₀) โดยเวลา t₁ เท่านั้น

โดยทั่วไปแล้ว จะแสดงในรูปแบบกราฟ โดยมีตำแหน่งทางกายภาพตามแกนแนวนอนและเวลาแสดงตามแนวแกนตั้ง โดยมีหน่วยเป็น t สำหรับเวลาและ ct สำหรับปริภูมิ (space) กรวยแสงในการแสดงนี้ปรากฏเป็นเส้นที่ 45 องศาโดยมีจุดศูนย์กลางอยู่ที่วัตถุ ขณะที่แสงเดินทางด้วยความเร็ว ct ต่อ t บนแผนภาพดังกล่าว ตำแหน่งที่เป็นไปได้ในอนาคตของวัตถุทั้งหมดจะอยู่ภายในกรวย

ดูเพิ่ม

• Timelike
• Causal structure
• Causality conditions
• Roman ring

อ้างอิง

• S. Carroll (2004). Spacetime and Geometry. Addison Wesley. ISBN 0-8053-8732-3.
• Kurt Gödel (1949). "An Example of a New Type of Cosmological Solution of Einstein's Field Equations of Gravitation". Rev. Mod,. Phys. 21 (3): 447. Bibcode:1949RvMP...21..447G. doi:10.1103/RevModPhys.21.447.
• W. Bonnor; B.R. Steadman (2005). "Exact solutions of the Einstein-Maxwell equations with closed timelike curves". Gen. Rel. Grav. 37 (11): 1833. Bibcode:2005GReGr..37.1833B. doi:10.1007/s10714-005-0163-3.

แหล่งข้อมูลอื่น

• A Primer on Time Travel (backup in the Internet Archive)