ฮีป (โครงสร้างข้อมูล)
ลิงก์ข้ามภาษาในบทความนี้ มีไว้ให้ผู้อ่านและผู้ร่วมแก้ไขบทความศึกษาเพิ่มเติมโดยสะดวก เนื่องจากวิกิพีเดียภาษาไทยยังไม่มีบทความดังกล่าว กระนั้น ควรรีบสร้างเป็นบทความโดยเร็วที่สุด |
| ฮีป | |
|---|---|
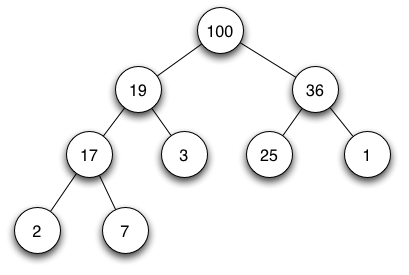 รูปแบบการเรียงตัวของฮีปทวิภาค (binary heap) โดยสมาชิกที่สำคัญกว่า (ในที่นี้เป็นฮีปมากสุดคือเลขที่มีค่ามากจะสำคัญ) จะอยู่ด้านบน | |
| ความสำคัญของลำดับ | FIFO (First In First Out) แต่เรียงตามลำดับความสำคัญ |
| การซ้ำกันของสมาชิก | อนุญาตให้ซ้ำกันได้ |
| เวลาที่ใช้ในการเข้าถึง | O(log n) |
| การทำให้ว่าง | ทำให้ทุกตัวเป็น null |
| เวลาที่ใช้ทำให้ว่าง | O(n) |
ฮีป (อังกฤษ: Heap) เป็นโครงสร้างข้อมูลที่นำมาสร้างแถวคอยลำดับความสำคัญ (priority queue) รูปแบบหนึ่ง ซึ่งนิยมใช้กันมาก โดยฮีปที่สร้างขึ้นโดยอาศัยแนวคิดจากต้นไม้ทวิภาคใช้ชื่อว่า "ฮีปทวิภาค" (binary heap) ซึ่งยังมีการสร้างฮีปโดยอาศัยแนวคิดแบบอื่น ๆ ได้อีกเช่น ฟีโบนักชีฮีป (fibonacci heap) โดยฮีปทุกชนิดนั้นมีความสัมพันธ์เหมือนกันคือปมพ่อมีลำดับความสำคัญมากกว่าปมลูก
แนวคิดของฮีปนอกจากนำมาสร้างแถวคอยลำดับความสำคัญแล้ว ยังนำมาประยุกต์ใช้ในการสร้างโครงสร้างข้อมูลอื่นๆ เช่นทรีพ เป็นต้น
ลักษณะของฮีป
[แก้]ฮีปเป็นต้นไม้ประเภทหนึ่งซึ่งจะจัดความสัมพันธ์ให้ปมพ่อ มีความสำคัญ(priority)มากกว่าปมลูก
ฮีปรูปแบบต่างๆ
[แก้]- ฮีปเติมเต็ม (completed heap) นอกจากที่จะเป็นฮีปแล้ว ยังเป็นต้นไม้เติมเต็ม(comleted tree)อีกด้วย ซึ่งฮีปประเภทนี้จะสามารถสร้างได้ด้วยแถวลำดับ
- ฮีปน้อยสุด (least heap) เป็นฮีปที่แทนความสำคัญด้วยตัวเลข โดยตัวเลขยิ่งน้อยจะยิ่งมีความสำคัญมาก เมื่อเขียนในรูปต้นไม้จะเหมือนว่าปมพ่อจะมีเลขความสำคัญน้อยกว่าปมลูกเสมอ
- ฮีปมากสุด (most heap) เป็นฮีปที่แทนความสำคัญด้วยตัวเลข โดยตัวเลขยิ่งมากจะยิ่งมีความสำคัญมาก เมื่อเขียนในรูปต้นไม้จะเหมือนว่าปมพ่อจะมีเลขความสำคัญมากกว่าปมลูก
- ทรีพ (treap) เป็นโครงสร้างข้อมูลที่สร้างข้อมูลเสริมให้มีความสัมพันธ์แบบฮีป ส่วนข้อมูลหลักจะเรียงความสัมพันธ์แบบต้นไม้ค้นหาแบบทวิภาค
จุดเด่นของฮีป
[แก้]ฮีปมีจุดเด่นในการเรียงลำดับในลักษณะต้นไม้ โดยเมื่อเรียงแล้วสมาชิกที่มีความสำคัญสูงสุดจะอยู่สูงสุดหรือเป็นราก ทำให้เข้าถึงข้อมูลที่มีความสำคัญสูงได้ง่าย อีกทั้งการเรียงแบบต้นไม้ โดยเฉพาะฮีปเติมเต็มด้วยแล้ว จึงสามารถลดเวลาการเข้าถึงลงเป็น O(log n)
บริการที่มักจะมี
[แก้]บริการนั้นจะเน้นบริการเดียวกับแถวคอยลำดับความสำคัญ
- เพิ่มรายการแนบด้วยระดับไว้ในแถวคอย (enqueue)
- ลบรายการที่มีความสำคัญสูงสุดและคืนค่านั้นกลับมา (prioritized dequeue)
- ดึงค่ารายการที่มีความสำคัญสูงสุดโดยไม่ลบรายการนั้นออก (peek)
ความเร็วที่ใช้ในการทำงาน
[แก้]จากการที่ฮีปเรียงตัวในลักษณะต้นไม้ โดยเฉพาะฮีปเติมเต็ม ทำให้ต้นไม้ที่ได้เป็นต้นไม้ประกันความสูง จึงเป็นการประกันการทำงานว่าอย่างมากจะใช้เวลา O(log n) และเข้าถึงข้อมูลที่สำคัญที่สุดได้ง่ายเพราะอยู่บนรากเป็นเวลาคงที่ O(1)
ประเภทข้อมูลที่ใช้สร้างฮีป
[แก้]เนื่องจากฮีปเป็นต้นไม้จึงอาจสร้างในลักษณะปมของต้นไม้ได้ ซึ่งใช้ประเภทข้อมูลประเภทโครงสร้าง หรือวัตถุ อย่างไรก็ตาม โดยปกติสำหรับการสร้างแถวคอยลำดับความสำคัญเราจะสร้างแบบฮีปเติมเต็ม ซึ่งสามารถใช้ความสัมพันธ์ทางคณิตศาสตร์ ทำให้เราสามารถใช้แถวลำดับในการสร้างฮีปเติมเต็มได้
ความสัมพันธ์ระหว่างดัชนีของปมพ่อและปมลูกในแถวลำดับของฮีปเติมเต็ม
[แก้]เมื่อเราแวะผ่านฮีปเติมเต็มตามความกว้าง(bread-first search)และเรียงเป็นแถวลำดับแล้ว เราจะได้ความสำคัญที่ว่าสำหรับสมาชิกดัชนีที่ i ใดๆ
- ปมพ่อของสมาชิกตัวนี้อยู่ที่
- ปมลูกทั้งสองตัวของสมาชิกตัวนี้อยู่ที่
การสร้างบริการของฮีป
[แก้]ในที่นี้กล่าวถึงลักษณะการทำงานของฮีปเติมเต็มในการทำแถวคอยลำดับความสำคัญ สำหรับการทำงานของทรีพให้ดูทรีพ#การสร้างบริการของทรีพ
การเข้าแถวคอย
[แก้]ทำได้โดยการเพิ่มสมาชิกไปที่หลังสุดของแถวลำดับก่อน และทำการสลับข้อมูลกับปมพ่อ(percolate up)เมื่อข้อมูลใหม่มีลำดับความสำคัญมากกว่า จนกระทั่งปมพ่อมีลำดับความสำคัญมากกว่าจึงหยุด
การลบสมาชิกที่สำคัญที่สุด
[แก้]ทำได้โดยการดึงเอาข้อมูลแรกสุดของแถวลำดับ กล่าวคือเป็นรากของฮีปเติมเต็ม ซึ่งจะมีลำดับความสำคัญมากที่สุดออก จากนั้นจะหยิบตัวสุดท้ายของแถวลำดับมาแทน (ซึ่งมักจะมีลำดับความสำคัญน้อย)และทำการลดลำดับลงโดยการสลับข้อมูลกับปมลูก(percolate down)จนข้อมูลสลับจนปมลูกมีลำดับความสำคัญน้อยกว่าจึงหยุด


