พาย (ค่าคงตัว)

สำหรับความหมายอื่น ดูที่ พาย

สัญลักษณ์ของพาย

พาย หรือ ไพ (อักษรกรีก: π ภาษาอังกฤษ: pi)เป็นค่าคงตัวทางคณิตศาสตร์ ที่เกิดจากความยาวเส้นรอบวงหารด้วยเส้นผ่านศูนย์กลางของวงกลม ค่า π มักใช้ในคณิตศาสตร์, ฟิสิกส์ และวิศวกรรม π เป็นอักษรกรีกที่ตรงกับตัว "p" ในอักษรละติน มีชื่อว่า "pi" (อ่านว่า พาย ในภาษาอังกฤษ แต่อ่านว่า พี ในภาษากรีก) บางครั้งเรียกว่า ค่าคงตัวของอาร์คิมิดีส (Archimedes' Constant) หรือจำนวนของลูดอล์ฟ (Ludolphine number หรือ Ludolph's Constant)

ในเรขาคณิตแบบยุคลิด π มีนิยามว่าเป็นอัตราส่วนของเส้นรอบวงหารด้วยเส้นผ่านศูนย์กลางของวงกลม หรือเป็นอัตราส่วนของพื้นที่วงกลม หารด้วย รัศมียกกำลังสอง ในคณิตศาสตร์ชั้นสูงจะนิยาม π โดยใช้ฟังก์ชันตรีโกณมิติ เช่น π คือจำนวนบวก x ที่น้อยสุดที่ทำให้ sin (x) = 0

การเกิดค่าพาย

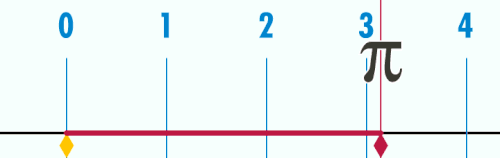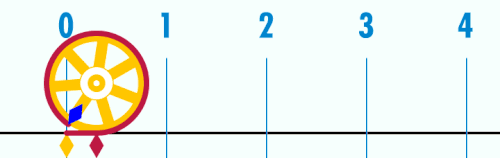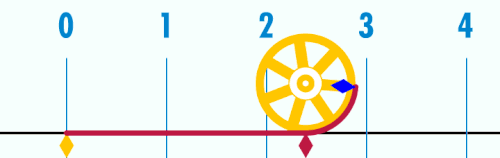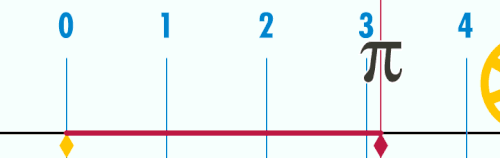
ค่า π โดยประมาณ 125 ตำแหน่งคือ

π = 3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328238644709384... (ลำดับ  A000796)

ส่วนมากจะใช้ค่าประมาณ คือ 3.14159...

แม้ว่าค่านี้มีความละเอียดพอที่จะใช้ในงานวิศวกรรมหรือวิทยาศาสตร์แล้ว ปัจจุบันมีการคำนวณค่า π ได้หลายตำแหน่ง ซึ่งหาได้ทั่วไปจากอินเทอร์เน็ต คอมพิวเตอร์ส่วนบุคคลโดยทั่วไปสามารถคำนวณค่า π ได้พันล้านหลัก ขณะที่ซูเปอร์คอมพิวเตอร์คำนวณค่า π ได้เกินล้านล้านหลัก และไม่พบว่ามีรูปแบบที่ซ้ำกันของค่า π ปรากฏอยู่

สูตรที่เกี่ยวข้องกับ π

สามารถคำนวณไพได้จาก เซตม็องแดลโบรต, โดยการคำนวณจำนวน iterations required before point (−0.75, ε) diverges.

เรขาคณิต

π มักปรากฏในสูตรที่เกี่ยวกับวงกลมและทรงกลม

รูปร่างทางเรขาคณิต	สูตร
เส้นรอบวงของวงกลมที่มีรัศมี r และเส้นผ่านศูนย์กลาง d	$C=\pi d=2\pi r\,\!$
พื้นที่ของวงกลมที่มีรัศมี r	$A=\pi r^{2}\,\!$
พื้นที่ของวงรีที่มีแกนเอก a และแกนโท b	$A=\pi ab\,\!$
ปริมาตรของทรงกลมที่มีรัศมี r และเส้นผ่านศูนย์กลาง d	$V={\frac {4}{3}}\pi r^{3}={\frac {1}{6}}\pi d^{3}\,\!$
พื้นที่ผิวของทรงกลมที่มีรัศมี r	$A=4\pi r^{2}\,\!$
ปริมาตรของทรงกระบอกที่สูง h และรัศมี r	$V=\pi r^{2}h\,\!$
พื้นที่ผิวของทรงกระบอกที่สูง h และรัศมี r	$A=2(\pi r^{2})+(2\pi r)h=2\pi r(r+h)\,\!$
ปริมาตรของกรวยที่สูง h และรัศมี r	$V={\frac {1}{3}}\pi r^{2}h\,\!$
พื้นที่ผิวของกรวยที่สูง h และรัศมี r	$A=\pi r{\sqrt {r^{2}+h^{2}}}+\pi r^{2}=\pi r(r+{\sqrt {r^{2}+h^{2}}})\,\!$

การวิเคราะห์

• François Viète, 1593:

${\frac {2}{\pi }}={\frac {\sqrt {2}}{2}}{\frac {\sqrt {2+{\sqrt {2}}}}{2}}{\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\ldots$

• สูตรของไลบ์นิซ:

${\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-\cdots ={\frac {\pi }{4}}$

หรือเขียนอีกแบบได้เป็น:

$\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}={\frac {\pi }{4}}$

• ผลคูณของ Wallis:

${\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots ={\frac {\pi }{2}}$

$\prod _{n=1}^{\infty }{\frac {(2n)^{2}}{(2n)^{2}-1}}=\prod _{n=1}^{\infty }{\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}={\frac {\pi }{2}}$

• สูตรปริพันธ์จากแคลคูลัส:

$\int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}$

• ปัญหาของBasel, ถูกแก้เป็นครั้งแรกโดย ออยเลอร์ (ดูเพิ่มเติม ฟังก์ชันซีตาของรีมันน์):

$\zeta (2)={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots ={\frac {\pi ^{2}}{6}}$

$\zeta (4)={\frac {1}{1^{4}}}+{\frac {1}{2^{4}}}+{\frac {1}{3^{4}}}+{\frac {1}{4^{4}}}+\cdots ={\frac {\pi ^{4}}{90}}$

• ฟังก์ชันแกมมา เมื่อหาค่า 1/2:

$\Gamma \left({1 \over 2}\right)={\sqrt {\pi }}$

• สูตรของสเตอร์ลิง:

$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}$

• เอกลักษณ์ของออยเลอร์ (เรียกโดย ริชาร์ด ไฟน์แมน):

$e^{i\pi }+1=0\;$

เศษส่วนต่อเนื่อง

π เขียนในรูปเศษส่วนต่อเนื่องได้หลายแบบ เช่น

${\frac {4}{\pi }}=1+{\frac {1}{3+{\frac {4}{5+{\frac {9}{7+{\frac {16}{9+{\frac {25}{11+{\frac {36}{13+...}}}}}}}}}}}}$

ทฤษฎีจำนวน

• ความน่าจะเป็นในการสุ่มจำนวนเต็มขึ้นมา 2 จำนวน แล้วเป็นจำนวนเฉพาะสัมพัทธ์กัน เท่ากับ 6/π² ...

ฟิสิกส์

• หลักการความไม่แน่นอนของไฮเซนเบิร์ก:

$\Delta x\Delta p\geq {\frac {h}{4\pi }}$

• สมการสนามของไอน์สไตน์ ในทฤษฎีสัมพัทธภาพทั่วไป:

$R_{ik}-{g_{ik}R \over 2}+\Lambda g_{ik}={8\pi G \over c^{4}}T_{ik}$

• กฎของคูลอมบ์ สำหรับแรงไฟฟ้า:

$F={\frac {\left|q_{1}q_{2}\right|}{4\pi \epsilon _{0}r^{2}}}$

สูตรที่นอกเหนือจากคณิตศาสตร์

การอธิบายปรากฏการณ์ทางกายภาพ

แม้ว่า π จะไม่เป็นค่าคงตัวทางฟิสิกส์ แต่ก็มีปรากฏในสมการที่ใช้อธิบายเกี่ยวกับหลักการพื้นฐานของจักรวาลอยู่บ่อยครั้ง เนื่องจากความสัมพันธ์ของ π กับวงกลม และระบบพิกัดทรงกลม จากสูตรง่าย ๆ จากกลศาสตร์ดั้งเดิม เช่น ให้ระยะเวลาโดยประมาณเป็น T ของลูกตุ้มที่มีความยาว L แกว่งด้วยแอมพลิจูดขนาดเล็ก (g คือ ความเร่งโน้มถ่วงของโลก)

$T\approx 2\pi {\sqrt {\frac {L}{g}}}$

หนึ่งในสูตรสำคัญของกลศาสตร์ควอนตัมคือหลักความไม่แน่นอนของไฮเซนแบร์ก ซึ่งแสดงให้เห็นความไม่แน่นอนในการวัดตำแหน่งของอนุภาค (Δx) และโมเมนตัม (Δp) ซึ่งไม่สามารถมีขนาดเล็กโดยปราศจากเหตุผลในเวลาเดียวกันได้ (เมื่อ h เป็นค่าคงตัวของพลังค์)

$\Delta x\,\Delta p\geq {\frac {h}{4\pi }}$

ความจริงที่ว่า π มีค่าประมาณเท่ากับ 3 นั้น มีบทบาทในอายุการใช้งานที่ยาวนานของออร์โธโพสิโทรเนียม ซึ่งอายุการใช้งานนั้นจะผกผันไปสู่ลำดับต่ำสุดในค่าคงที่โครงสร้างละเอียด α คือ

${\frac {1}{\tau }}=2{\frac {\pi ^{2}-9}{9\pi }}m\alpha ^{6},$

เมื่อ m คือมวลของอิเล็กตรอน

ดูเพิ่ม

• แคลคูลัส
• เรขาคณิต
• ฟังก์ชันตรีโกณมิติ