ค่าคงที่กรวย

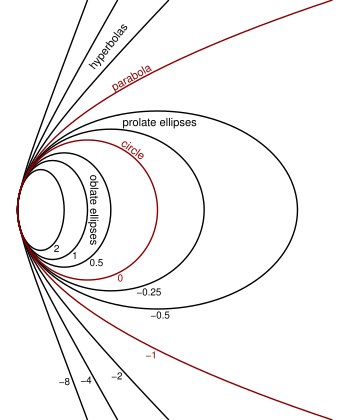
ใน เรขาคณิต ค่าคงที่กรวย (หรือ ค่าคงที่ชวาร์สชิลด์^[1] ตาม คาร์ล ชวาร์สชิลด์) เป็นปริมาณที่เป็นปริมาณที่อธิบายภาคตัดกรวยและแสดงด้วยตัวอักษร Kค่าคงที่นี้กำหนดโดย K ค่าคงที่นี้กำหนดโดย $K=-e^{2},$ โดยที่ $e$ คือ ความเยื้องศูนย์กลาง ของหน้าตัดกรวย

สมการของภาคตัดกรวยที่มีจุดยอดที่ จุดกำเนิด และสัมผัสแกน y คือ $y^{2}-2Rx+(K+1)x^{2}=0$ หรือ $x={\dfrac {y^{2}}{R+{\sqrt {R^{2}-(K+1)y^{2}}}}}$ โดยที่ R คือ รัศมีความโค้ง ที่ $x = 0$

การกำหนดนี้ใช้ใน ทัศนศาสตร์เรขาคณิต เพื่อระบุพื้นผิวเลนส์และกระจกที่เป็นรูป ทรงรีแบน ( $K > 0$ ), ทรงกลม ( $K = 0$ ), ทรงรียาว ( $0 > K > -1$ ), พาราโบลอยด์ ( $K = -1$ ), และ ไฮเพอร์โบลอยด์ ( $K < -1$ ) เมื่อ การประมาณค่าแบบพาราเซียล ถูกต้อง พื้นผิวออปติกสามารถถือเป็นพื้นผิวทรงกลมที่มีรัศมีเท่ากันได้

อ้างอิง

↑ Rakich, Andrew (2005-08-18). Sasian, Jose M; Koshel, R. John; Juergens, Richard C (บ.ก.). "The 100th birthday of the conic constant and Schwarzschild's revolutionary papers in optics". Novel Optical Systems Design and Optimization VIII. International Society for Optics and Photonics. 5875: 587501. Bibcode:2005SPIE.5875....1R. doi:10.1117/12.635041. S2CID 119718303.

Smith, Warren J. (2008). Modern Optical Engineering, 4th ed. McGraw-Hill Professional. pp. 512–515. ISBN 978-0-07-147687-4.

บทความนี้ยังเป็นโครง คุณสามารถช่วยวิกิพีเดียได้โดยการเพิ่มเติมข้อมูล

หมายเหตุ: ขอแนะนำให้จัดหมวดหมู่โครงให้เข้ากับเนื้อหาของบทความ (ดูเพิ่มที่ วิกิพีเดีย:โครงการจัดหมวดหมู่โครงที่ยังไม่สมบูรณ์)

[1] Rakich, Andrew (2005-08-18). Sasian, Jose M; Koshel, R. John; Juergens, Richard C (บ.ก.). "The 100th birthday of the conic constant and Schwarzschild's revolutionary papers in optics". Novel Optical Systems Design and Optimization VIII. International Society for Optics and Photonics. 5875: 587501. Bibcode:2005SPIE.5875....1R. doi:10.1117/12.635041. S2CID 119718303.

[1]